به باور یونانیان باستان، ارتباط عمیقی بین موسیقی و ریاضی وجود داشته است. از دوران باستان، توجه محققان به قواعد و تناسبات بین اعداد و موسیقی بوده است. فیثاغورث، فیلسوف و ریاضیدان یونانی، از نخستین افرادی بود که رابطه موسیقی و ریاضی را در بررسی تارهای صوتی مورد بررسی قرار داد.
در مطالعاتی که ارتباط موسیقی و ریاضی را بررسی میکنند، میتوان معیارهای مشخصی را تعریف کرد. کشف ارتباط بین موسیقی و ریاضی و تعیین مرزبندی و نقاط مشترک بین این دو هدف این موضوع است.
در این مطلب، ارتباط موسیقی و ریاضی از چند دیدگاه مورد ارزیابی قرار میگیرد. یکی از این موارد نشان دادن الگوهای ریاضی در آهنگسازی است. دیدگاه دیگر مربوط به هارمونی بین نتها و ارتباط آن با کوک کردن ساز است که با توجه به باور یونانیان باستان، ارتباط مستقیمی با علم ریاضی دارد.
سمفونی ریاضی و یادگیری موسیقی
موسیقی و ریاضیات از دورانهای گذشته در یک رابطه پیچیده و هماهنگ با یکدیگر تنیده شدهاند و ارتباط عمیقی دارند که مورد توجه دانشمندان، موسیقیدانان و مربیان قرار گرفته است. اگرچه به نظر میرسد که این دو رشته متمایز باشند، اما اصول اساسی ریاضیات نقش مهمی در ایجاد، درک و تحلیل موسیقی دارند. در این بحث، ما به بررسی رابطه چند وجهی بین ریاضیات و موسیقی میپردازیم و نشان میدهیم که چگونه مفاهیم ریاضی به عنوان پایهای برای جنبههای مختلف تئوری، ترکیب و اجرای موسیقی عمل میکنند. در این سفر، ما خواهیم فهمید که چگونه ریاضیات به عنوان یک ابزار قدرتمند برای یادگیری و مسلط شدن بر هنر موسیقی عمل میکند.
تحقیقات نشان میدهد که کودکانی که توانایی نواختن پیانو را دارند، مهارتهای استدلالی بهتری را در انجام تمرینهای ریاضی و بازیهایی مانند شطرنج و جور چین دارند. علاوه بر این، بررسیهای دیگر نشان میدهد که دانشجویان رشته ریاضی که در دانشگاه در دوره کارشناسی موسیقی را مطالعه کردهاند، بهترین مسائل ریاضی را درک میکنند نسبت به همسالانشان که موسیقی را مطالعه نکردهاند.
از دوران بسیار قدیم، ریاضیدانان تمایل زیادی به موسیقی و یادگیری آن داشتهاند. به طور کلی، تاثیر موسیقی بر یادگیری ریاضی موضوعی نو و جدید نیست و آموزگاران از قرنهای پیش از این از نقش اساسی موسیقی در رشد ذهن انسان در مسائل ریاضی آگاه بودهاند.
نقش موسیقی در تقویت مهارتهای ریاضی
بسیاری از افراد فقط به جنبه هنری موسیقی توجه میکنند، اما واقعیت این است که موسیقی دارای یک رابطه عمیق و تنگانگی با ریاضی است.
نه تنها نتها و اصوات مربوط به موسیقی از لحاظ شدت و بسامد با ریاضی ارتباط دارند، بلکه این ارتباط بسیار گسترده است و میتوان تمام یک قطعه موسیقی را از نظر روابط ریاضی مورد بررسی قرار داد. موسیقیدانان باور دارند که تعادل و هماهنگی زیادی بین موسیقی و علم ریاضی وجود دارد.
موسیقی، که در مرکز آن صدای سازمان یافته است، و ریاضیات، که چارچوب اساسی برای درک و بیان این سازمان را فراهم میکند، به طور نزدیک با یکدیگر ارتباط دارند. اساس نتهای موسیقی، که یک سیستم برای نمایش ایدههای موسیقی روی کاغذ استفاده میشود، به شدت بر مفاهیم ریاضی متکی است. بلوکهای اصلی موسیقی، مانند نتها و ریتمها، میتوانند به عنوان موجودیتهای ریاضی در نظر گرفته شوند.
به عنوان مثال، در نظر بگیرید مفهوم مدت زمان یک نت موسیقی که اغلب با ضربات اندازهگیری میشود. یک نت کامل معمولاً به عنوان داشتن چهار ضربه تعریف میشود، در حالی که نیم نت دارای دو و یک چهارم نت یک است. این تقسیم زمان ذاتاً ریاضی است و از کسرها برای نمایش مدت زمانهای مختلف استفاده میکند. رابطه بین این مقادیر نت – یعنی چگونگی ترکیب، تقسیم و مرتب کردن آنها – اساس ریتم را تشکیل میدهد که اساساً مطالعه ریاضی زمان و تقسیمات آن است.
نقش ریاضی در خلق هارمونی
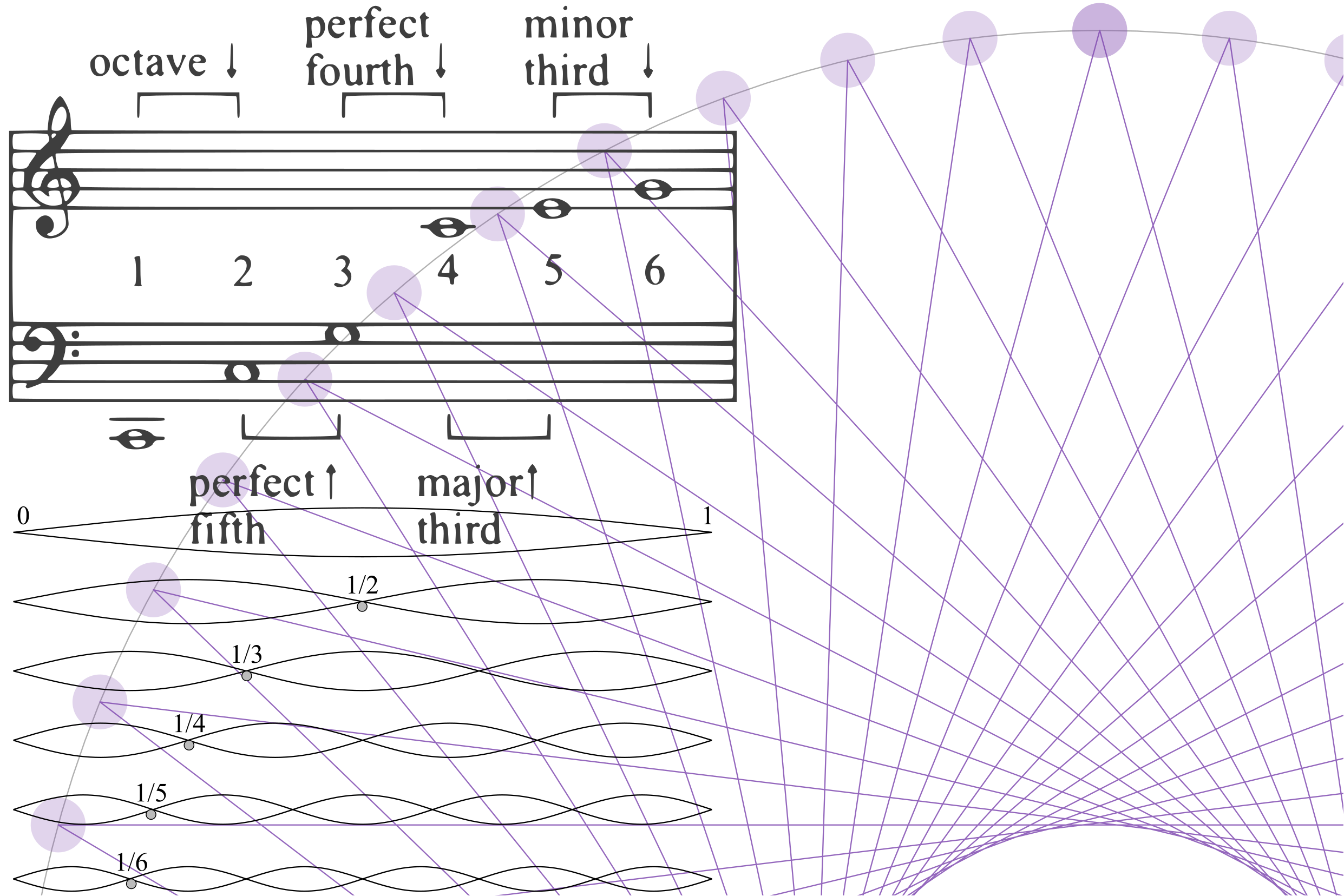
هارمونی موسیقی، که هنر ترکیب نتهای مختلف برای ایجاد صداهای دلنشین و معنادار است، عمیقاً ریشه در نسبتهای ریاضی دارد. سادهترین و اساسیترین رابطه در موسیقی اکتاو است که در آن یک نت دو برابر فرکانس دیگری است. این دو برابر شدن فرکانس مربوط به نسبت 2:1 است که یک مفهوم اساسی ریاضی است.
فواصل دیگر مانند پنجم و چهارم را میتوان از نظر نسبتها نیز فهمید. به عنوان مثال، یک پنجم کامل با نسبت فرکانس 3:2 مطابقت دارد، در حالی که یک چهارم کامل مربوط به نسبت 4:3 است. این نسبتها همخوانی دلپذیر این فواصل را تعیین میکنند و اساس مقیاسها و آکوردهای موسیقی هستند.
مطالعه هارمونیکها یا تونها نیز بر اصول ریاضی تکیه دارد. وقتی یک آلت موسیقی یک نت تولید میکند، فقط یک لحن خالص تولید نمیکند. در عوض، موج پیچیدهای تولید میکند که از هارمونیکهای متعدد تشکیل شده است که هر کدام فرکانس و دامنه خاص خود را دارند. این هارمونیکها مضرب صحیح فرکانس پایه هستند و میتوان آنها را با استفاده از معادلات ریاضی مانند سری فوریه توصیف کرد.
موسیقی زبانی هندسی
یکی از جذابترین ارتباطهایی که بین ریاضیات و موسیقی وجود دارد، در زمینهٔ هندسه موسیقی است. یکی از نمونههای معروف این تلاقی، مطالعهٔ “دایرهٔ پنجم” است که یک نمایش هندسی از روابط موسیقی است. در این دایره، هر کلید در یک زاویهٔ خاص قرار دارد و حرکت در اطراف دایره معادل حرکت در یک پنجم یا چهارم است. ماهیت هندسی این دایره به نوازندگان کمک میکند تا روابط کلیدی، پیشرفت آکورد و مدولاسیون را درک کنند.
به طور مشابه، میتوان الگوهای موسیقی را با استفاده از تحلیل و تبدیلهای ریاضی بررسی کرد. به عنوان مثال، هندسهٔ فراکتال برای درک و ایجاد آهنگهای پیچیدهٔ موسیقی استفاده شده است. فراکتالها، که شکلهای هندسی خود را تکرار میکنند، میتوانند برای تولید موتیفهای موسیقی که خود در مقیاسهای مختلف شباهتی را نشان میدهند، مورد استفاده قرار گیرند.

نقش ریاضیات در ترکیب
آهنگسازان اغلب از روشهای ریاضی برای ساختاردهی موسیقی خود و ایجاد ترکیبات پیچیده استفاده میکنند. یکی از این روشها، استفاده از دنباله فیبوناچی است که مجموعهای از اعداد است که در آن هر عدد، مجموع دو عدد قبلی است؛ به عنوان مثال، 0، 1، 1، 2، 3، 5، 8، 13 و …
آهنگسازان از دنباله فیبوناچی برای تعیین عناصری مانند طول بخشها، تعداد تکرارها و حتی انتخاب فواصل موسیقی استفاده میکنند. به علاوه، ساختارهای ریاضی مانند الگوریتمها و ماتریسها نیز برای تولید عناصر موسیقایی بهکار میروند. ترکیب الگوریتمی شامل استفاده از قوانین ریاضی برای تولید الگوهای موسیقی است، در حالی که نتنویسی ماتریسی به آهنگسازان اجازه میدهد تا عناصر موسیقی را به طور سیستماتیک دستکاری کنند.
تاثیر موسیقی بر هوش و حافظه
ارتباط بین ریاضی و موسیقی به ابعاد فراتر از مفاهیم نظری و تکنیکهای آهنگسازی میرسد. پژوهشها نشان دادهاند که یادگیری موسیقی، سازندهترین آن نواختن یک ساز یا خواندن آواز، تأثیرات قابل توجهی بر رشد شناختی افراد دارد، بهویژه در زمینه ریاضیات.
تحقیقات نشان میدهند که آموزش موسیقی میتواند تواناییهای ریاضی را در کودکان تقویت کند. یادگیری خواندن نت موسیقی شامل درک مفاهیمی مانند تشخیص الگو، توالی، و روابط فضایی است که همگی از مهارتهای اساسی در ریاضیات محسوب میشوند. بهعلاوه، جنبههای ریتمیک موسیقی به تقویت مفاهیم زمان و تناسب در ریاضیات کمک میکند.
تأثیرات متقابل موسیقی و اختلالات ریاضی
با توجه به اینکه موسیقی یکی از اهمیتهای برجسته برای بهبود ارتباط بین دو نیمکره چپ و راست مغز است، آموزش آن به کودکانی که با درک مفاهیم ریاضی مشکل دارند، به عنوان یک ابزار موثر و کارآمد مطرح میشود.
موسیقی با داشتن ساختار منظم، وزن، و هماهنگی دقیق، میتواند بهبودی چشمگیر در یادگیری مفاهیم ریاضی و عملکرد بهتر دانشآموزان ایجاد کند. از این رو، موسیقی میتواند به عنوان یک ابزار موثر برای تقویت مهارتهای مختلف درس ریاضی عمل کند.
نمادها و الگوهای موجود در موسیقی، اساسی و حیاتی برای درک بهتر مسائل ریاضی هستند. نواختن یک قطعه موسیقی، شباهتهای زیادی به حل مسائل ریاضی دارد و مفهوم آن با نمادهای معتبر در ارتباط است.
براساس تحقیقات انجام شده در این زمینه، دانشآموزانی که قبل از انجام فعالیتهای ریاضی، به یکی از قطعات موسیقی معروف گوش داده بودند، نسبت به همتایانی که به یک قطعه آرام گوش فرا داده بودند، عملکرد بهتری از خود نشان دادهاند.
تعامل بین ریاضی و موسیقی
ارتباط بین ریاضیات و موسیقی به عنوان یک رابطه چندوجهی و پربار، مورد توجه قرار میگیرد. ریاضیات، به عنوان زبان و ساختار اساسی، ابزارهایی را برای درک و خلق موسیقی فراهم میکند، از شناخت نمادهای موسیقی تا هماهنگی فواصل آنها. جنبههای هندسی و فراکتال ریاضیات نیز بینش منحصر به فردی را درباره الگوها و ترکیبات موسیقی ارائه میدهد.
همچنین، یادگیری موسیقی با مؤلفههای ریاضی ذاتی آن، میتواند به رشد شناختی، از جمله توانمندیهای ریاضی، کمک کند. آموزش موسیقی اغلب از مفاهیم ریاضی بهره میبرد تا فرایند یادگیری را برای دانشآموزان جذابتر و معنادارتر کند.
در واقع، ریاضی و موسیقی دو دامنه متمایز نیستند؛ بلکه به هم پیوسته و مترادف میباشند. همکاری بین این دو حوزه زندگی ما را بهطور قابل توجهی غنیتر میکند و توانایی درک عمیقی از زیبایی ریاضیات و تأثیرگذاری موسیقی بر روح انسان را به ما میآموزد. برای هر کسی، از ریاضیدانها تا موسیقیدانها، کشف این ارتباط میتواند به درک عمیقتری از هر دو حوزه کمک کند و راههای جدیدی را برای خلاقیت و یادگیری باز کند.
برای مطالعه مطالب متنوع با ما همراه باشید































نظرات کاربران