استاد فیزیک دانشگاه جنوب شرقی لوئیزیانا، رت آلن، با استفاده از قوانین فیزیک، تشریح میدهد که آیا سوسکی که از فضا به زمین سقوط کند، ممکن است زنده بماند یا خیر. او در وبسایت وایرد این سوال جالب را که در ردیت مطرح شده بود، به بررسی میپردازد. آلن توضیح میدهد که استراتوسفر تا ارتفاع ۵۰ کیلومتری از سطح زمین ادامه دارد. اما چگونه سوسکی که از فضا به زمین میافتد، با این شرایط مقابله میکند؟ با شروع از خط کارمان که ۱۰۰ کیلومتر بالای سطح زمین قرار دارد، آلن به بررسی این مسأله پرداخته و تا حد تقریبی پاسخی برای این سوال فیزیکی فراهم میآورد.
سقوط بدون هوا
همانطور که در بسیاری از مسائل دنیای واقعی اتفاق میافتد، فیزیک ممکن است به شدت پیچیده باشد. وقتی که فیزیکدانان در مورد سقوط یک سوسک فکر میکنند، اولین قدم آن است که مساله را سادهتر کنند. این کار یک نوع تقلب نیست، بلکه ابتدا باید یک پاسخ اولیه برای فکر کردن درباره مسأله بهدست آورده شود. بدیهی است که تعامل بین سوسک و هوا بزرگترین عامل پیچیدهکننده خواهد بود.
هوا نیروی فشاری به سمت عقب وارد میکند که با سرعت سوسک هماهنگ میشود. اگر تصور کنیم که سوسک در یک محیط بدون هوا سقوط میکند، مسأله به شدت سادهتر میشود.
تعامل هوا با یک جسم که در حال سقوط است، به شکل جسم بستگی دارد. اما در محاسبات ابتدایی، شکل جسم اهمیتی ندارد. بنابراین، میتوانیم به سادگی تصور کنیم که سوسک یک جسم گرد با جرم (m) و ارتفاع (h) از بالای زمین است. وقتی به زمین برخورد میکند، چه سرعتی خواهد داشت؟
اگر مثلاً سوسک یک گلوله را از بالای یک ساختمان بلند پرتاب کرده بودیم، میتوانستیم تصور کنیم که نیروی گرانش ثابت است و میتوانستیم مقدار آن را با ضرب در میدان گرانشی (g) محاسبه کنیم که برابر با ۹.۸ نیوتن بر کیلوگرم است. البته با افزایش ارتفاع از سطح زمین، دیگر نمیتوانیم فرض کنیم که میدان گرانشی ثابت باقی میماند.
استفاده از عبارت زیر میتواند به ما کمک کند تا مقدار g را محاسبه کنیم. در اینجا، G ثابت گرانش جهانی، ME جرم زمین، RE شعاع زمین و h ارتفاع بالای سطح قرار دارند.
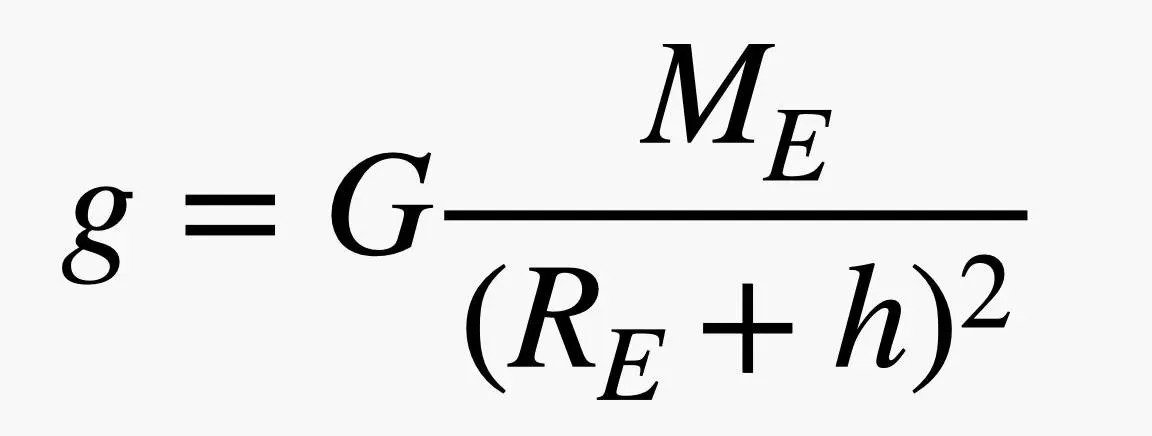
به دلیل اینکه شعاع زمین بسیار بزرگ است (۶٬۳۷۱٬۰۰۰ متر)، مخرج عبارت بالا اغلب توسط این مقدار غالب میشود. حتی با افزایش ارتفاع به ۱۰,۰۰۰ متر، میدان گرانشی با کاهش به ۹.۷۶ نیوتن بر کیلوگرم مواجه میشود و به نظر میرسد که عملکردی ثابت داشته باشد. اگرچه با افزایش ارتفاع تا ۱۰۰ کیلومتر، میدان گرانشی به ۹.۴۹ نیوتن بر کیلوگرم میرسد. بنابراین، برای مدلسازی نیاز به یک روش داریم که این نیروی متغیر را برای جسم در حال سقوط در نظر بگیرد، و دو راه برای انجام این کار وجود دارد.
روش اول، از قضیه کار-انرژی برای محاسبه سرعت نهایی با استفاده از تغییر پتانسیل گرانشی استفاده میکند. با این حال، وقتی هوا به معادله اضافه میشود، این روش کارآمد نمیباشد زیرا نمیتوان نیروی هوا را به عنوان انرژی مدل کرد. بنابراین، این راه حل بهترین گزینه ممکن نیست.
روش دوم، حرکت جسم در حال سقوط را به فواصل زمانی بسیار کوتاهی تقسیم میکند. فرض کنید هر بازه زمانی یک ثانیه طول میکشد. در طول هر یک از این بازهها، میتوانیم میدان گرانشی را به عنوان مقدار ثابت در نظر بگیریم. این به این معناست که میتوانیم از یک شکل ساده از فیزیک برای محاسبه تغییر در سرعت و موقعیت در طول هر بازه یک ثانیه استفاده کنیم.
برای مدلسازی حرکت در طول ۱۰۰ ثانیه، به ۱۰۰ محاسبه از این نوع نیاز داریم. برای انجام این محاسبات، راهحل سادهتر این است که کامپیوتر را وظیفه انجام تمام محاسبات پیچیده را بر عهده گیرد. میتوانید از هر زبان برنامهنویسی برای این محاسبات عددی استفاده کنید. نمودار زیر نشاندهنده سرعت جسم در حال سقوط است.
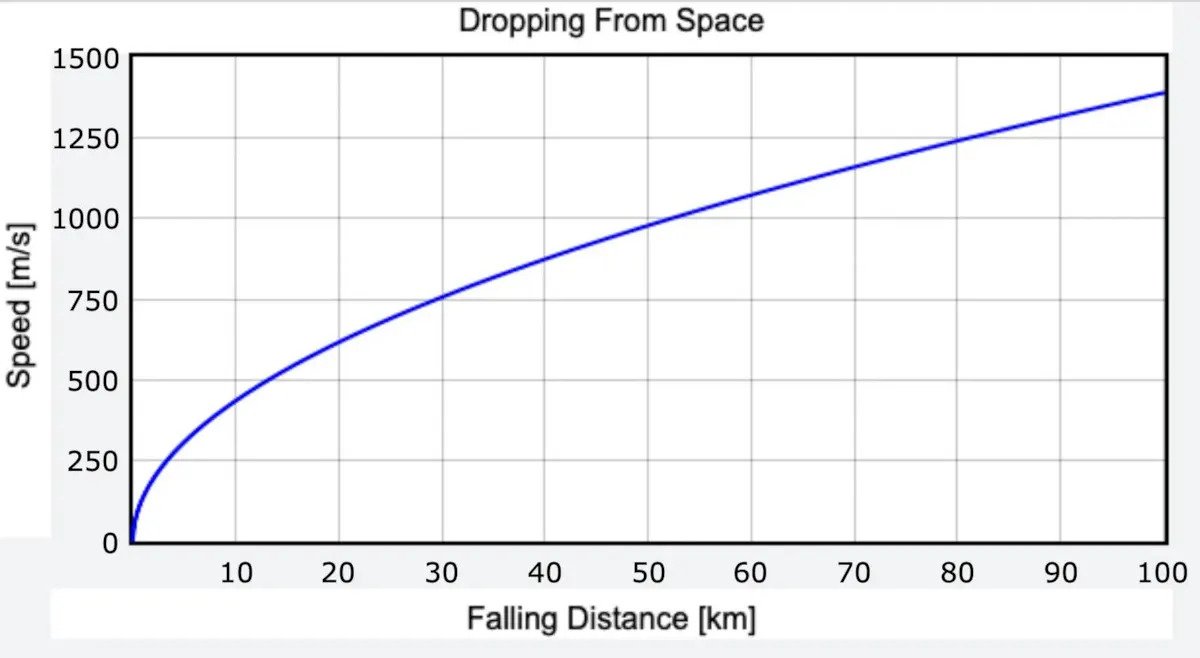
در لحظهی برخورد، جسم با سرعت ۱۳۸۹ متر بر ثانیه حرکت میکند، که بیشتر از سرعت سریعترین هواپیمای جت میباشد. این سرعت، با اینکه به نظر میرسد محاسبه ما بسیار واقعبینانه است، به دلیل کاهش مقاومت هوا از سرعت جسم در حال سقوط، به صورت واقعگرایانه نمیباشد. بنابراین، ضروری است تاثیر مقاومت هوا را نیز در محاسبات درنظر گرفت.
سقوط از میان هوا
میتوانیم ارتباط بین جسم متحرک و هوا را با مدلسازی نیروی درگ توضیح دهیم. نیروی درگ، بهطور شهودی، مشابه احساسی است که در زمانی که دست خود را از پنجره ماشین در حال حرکت بیرون میآورید و هوا برخلاف دست شما عمل میکند، به وجود میآید. میزان این نیرو با افزایش سرعت خودرو افزایش مییابد. حالا با استفاده از معادله زیر، این نیرو را به طور تقریبی محاسبه میکنیم:
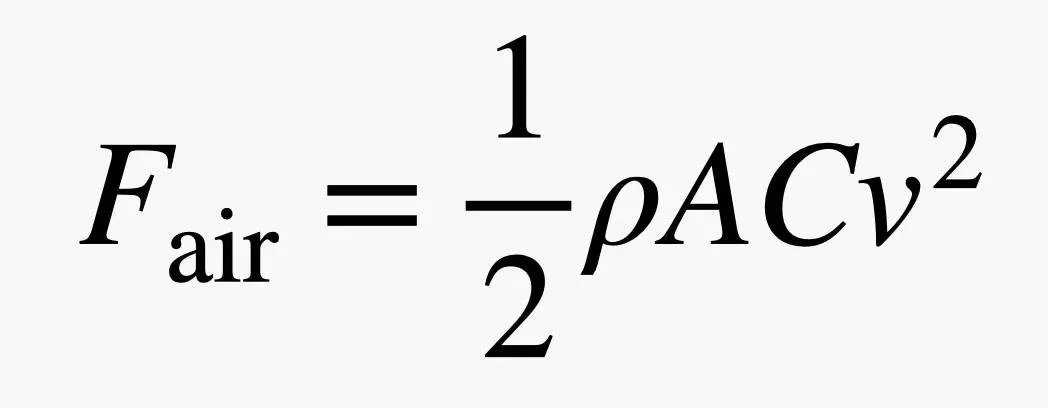
در معادله فوق، ρ به چگالی هوا، A به مساحت مقطع جسم (برای یک کره، مساحت دایرهای خواهد بود)، C به ضریب درگ که به شکل جسم بستگی دارد و v به سرعت جسم اشاره دارد. این مسائل محاسباتی چالشبرانگیزی دارد زیرا نیروی مقاومت هوا به سرعت بستگی دارد و سرعت نیز به نیرو بستگی دارد (مطابق با قانون دوم نیوتن). با این حال، با شکستن حرکت به بازههای زمانی کوتاه، میتوان نیروی درگ را به عنوان یک مقدار ثابت در طول این بازهها فرض کرد، که این مسئله را سادهتر میکند.
به همین ترتیب، چگالی هوا نیز با تغییر ارتفاع تغییر میکند. در نزدیکی سطح زمین، چگالی هوا حدود ۱٫۲ کیلوگرم بر متر مکعب است اما با افزایش ارتفاع، این مقدار کاهش مییابد. با این حال، با استفاده از یک مدل برای چگالی هوا به عنوان تابعی از ارتفاع، میتوان این مقدار را محاسبه کرد.
نکته دیگری که باید در نظر گرفته شود این است که اگر نیروی درگ هوا بر روی جسم حرکتی وجود نداشته باشد، کل نیرو به نیروی گرانش منتهی میشود که به جرم جسم متناسب است.
با توجه به قانون دوم نیوتن که نیروی خالص برابر با حاصل ضرب جرم و شتاب است (Fnet = ma)، این نیرو با جرم متناسب است. از اینرو، میتوانیم آن را با جرم ضربدر شتاب خنثی کنیم، بهطوریکه شتاب به جرم بستگی نداشته باشد. این امر به این معناست که در برخی موارد اجسام با جرمهای مختلف به زمین برخورد میکنند. با اینحال، اگر نیروی درگ هوا را اضافه کنیم، نیروی خالص نه تنها به جرم، بلکه به اندازه جسم نیز بستگی دارد. این به معنای این است که توپهای بولینگ و تنیس با حرکات متفاوتی سقوط میکنند.
با این توضیحات، حالا میتوانیم سه حالت را در نظر بگیریم: یک جسم بدون مقاومت هوا و سه جسم که دارای مقاومت هوا هستند؛ به عبارت دیگر، سوسک، توپ تنیس و توپ بولینگ. این انتخاب برای بررسی سقوط اجسام کروی با اندازههای مختلف مناسب است.
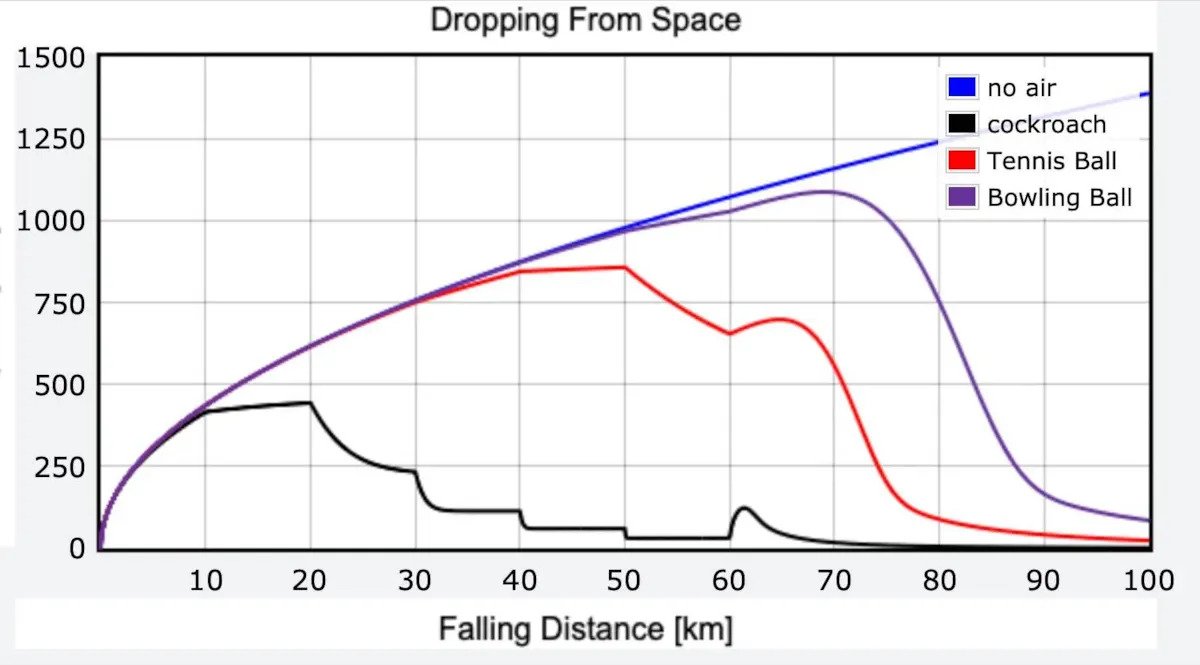
توجه داشته باشید که هنگامی که اجسام دارای مقاومت هوا به ارتفاعات فوقانی از جو میرسند و با یک محیط با مقاومت هوای بسیار کم روبرو میشوند، سرعت آنها به سرعتهای بسیار بالا افزایش مییابد. با این حال، زمانی که وارد محیط با هوای چگالتر میشوند، سرعت آنها کاهش مییابد. سرعت سوسک به دلیل دقت پایین مدل چگالی هوای من در ارتفاعات بالا، بهطور قابل توجهی کاهش مییابد. با این وجود، تمام اجسام در نهایت به سرعت نهایی خود میرسند.
در مورد توپ بولینگ، سرعت نهایی آن ۸۳ متر بر ثانیه است، در حالیکه سوسک به سرعت نهایی تنها ۱٫۵ متر بر ثانیه میرسد. توپ تنیس با سرعت نهایی ۲۳٫۸ متر بر ثانیه میان این دو قرار دارد. از نظر بقا، به نظر میرسد سوسک با مشکلی مواجه نمیشود. احتمالاً به یاد دارید که سوسکها میتوانند به راحتی سریعتر از شما حرکت کنند. اگر بتوانند با این سرعت روی سطح زمین حرکت کنند، احتمالاً از برخورد با زمین با این سرعت جان سالم به در خواهند برد.
توپ تنیس نیز مشکلی ندارد؛ سرعت نهایی آن چیزی است که میتوانید در طول یک بازی تنیس مشاهده کنید. با این حال، توپ بولینگ احتمالاً قادر به تحمل چنین سرعتی نخواهد بود و اگر با سطح سخت مانند سیمان یا خاک خشک و سفت برخورد کند، خراب خواهد شد. اما ممکن است از برخورد با یک سطح نرمتر مانند آب یا گل، جان سالم به در ببرد.
سقوط و گرما
اگر به مسائل مرتبط با اکتشافات فضایی توجه داشته باشید، مطلع هستید که زمانی که اشیاء با سرعت بسیار بالا وارد جو میشوند، داغ میشوند. برهمکنش بین جسم و هوا نیروی مقاومت به سمت عقب از سوی هوا ایجاد میکند، اما همچنین ممکن است هوای جلوی جسم در حرکت را هم فشرده کند. این هوا، داغ شده و سطح جلوی جسم در حال سقوط را گرم میکند. در مورد فضاپیماها در هنگام ورود مجدد، این گرما به حدی شدید میشود که نیاز به سپر حرارتی دارد تا از ذوب شدن بخشهای دیگر آن جلوگیری شود.
حالا، چگونه اشیاء در حال سقوط با این شرایط مواجه میشوند؟ بهویژه زمانی که با هوای متحرک در سرعتهای بسیار بالا برخورد میکنند، موقعیت ممکن است پیچیده شود.
اگرچه این مسئله تنها بهعنوان یک موضوع سرگرمی مطرح شده و کاربردهای عملی در حوزه فضایی ندارد، ما میتوانیم از یک تقریب برای محاسبه گرما در طول سقوط استفاده کنیم. در ابتدا، میتوانیم کاری که توسط نیروی مقاومت هوا انجام شده را محاسبه کنیم. این کار اساساً حاصلضرب نیرو (که قبلاً محاسبه شده) در مسافت است. از آنجا که نیرو هماهنگ با سقوط جسم تغییر میکند، میتوانیم مقدار کار اندکی را در طول هر بازه زمانی کوچک محاسبه کرده و سپس آنها را باهم ترکیب کنیم. دوماً، فرض میکنیم که این کار هم هوا و هم جسم را گرم کرده و برای سادهتر کردن میتوان گفت که نیمی از انرژی به جسم منتقل میشود. در نهایت، میتوانیم ظرفیت گرمایی ویژه هر جسم را تقریب بزنیم. ظرفیت گرمایی ویژه رابطه بین انرژی وارد شده به جسم و تغییر دمای آن را نشان میدهد.
در این مقاله، هدف ما از اندازهگیری تجربی ظرفیت گرمایی ویژهی سوسک خودداری میشود.
با توجه به تخمینها، دمای توپ بولینگ تغییر دمای بیش از هزار درجه سانتیگراد را نشان میدهد و توپ تنیس از این نظر هم نیز وضعیت ناپسندتری دارد. محاسبات نشان میدهد که دمای توپ تنیس به ۱۷۰۰ درجه افزایش پیدا میکند. در صورت رسیدن هر یک از این توپها به این دما، نه تنها ذوب میشوند، بلکه تبخیر هم میشوند و هیچ چیزی برای برخورد با زمین باقی نمیماند.
در مورد سوسک، به نظر میرسد که با رسیدن به دمای ۹۶۰ درجه سانتیگراد، وضعیت آن نیز به شدت ناپایدار خواهد شد.
البته، فرض محاسبات ما این است که در هر بازه زمانی کوتاه، دمای جسم افزایش مییابد. این فرض اثر خنککننده حاصل از وارد شدن به هوای جدید را در نظر نمیگیرد. به جای آن، ما به بررسی افزایش دما به دلیل تعامل با هوا میپردازیم. در اینجا نمونهای از نرخ تغییر دما برای سه جسم را مشاهده میکنیم:
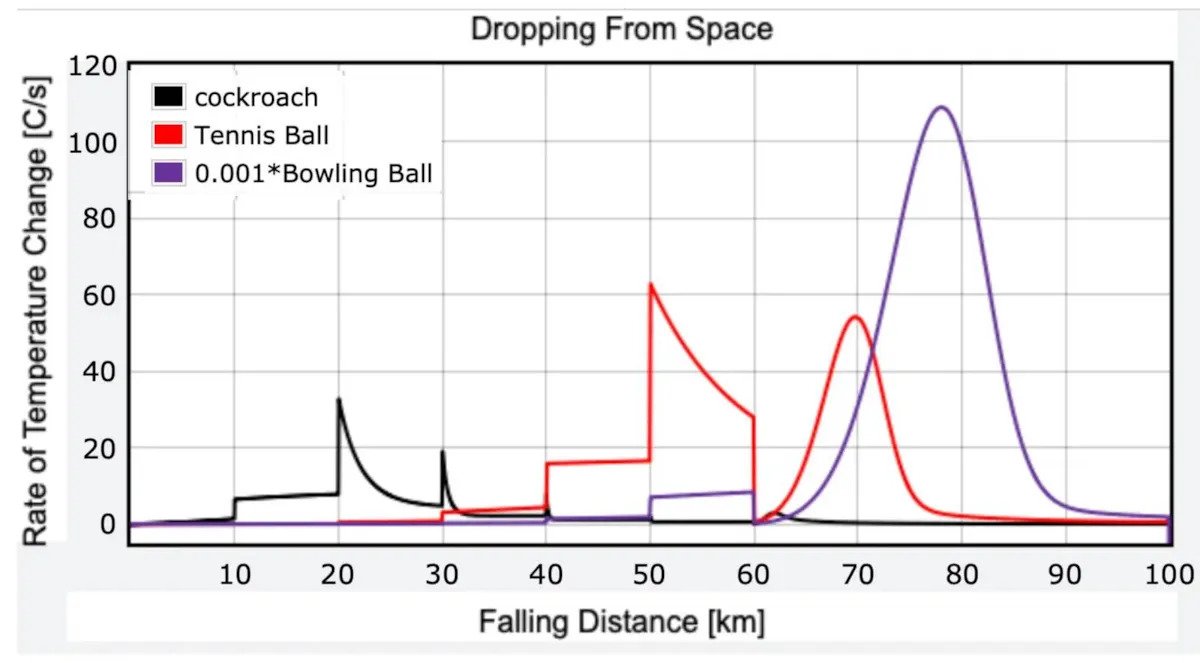
در نمودار فوق، مقیاس دادهها کاهش یافته است تا بتوانید جزئیات نرخ تغییر دما را برای توپ تنیس و سوسک به خوبی مشاهده نمایید.
نتایج به شدت ناامیدکننده است، حداقل برای آن دسته از ما که به سوسکها علاقه نداریم. لطفاً توجه داشته باشید که سوسک دورههای کوتاهی از افزایش دما را تجربه میکند (احتمالاً به دلیل ورود به هوای با تراکم بالاتر که در آن سرعت آن باید کاهش یابد). اما در طول مراحل دیگر سقوط، سوسک به طور چشمگیری گرم نمیشود. این امر فرصت زیادی برای خنک شدن ایجاد میکند و احتمال بقا را افزایش میدهد.
همین امر در مورد توپ تنیس نیز صدق میکند، اگرچه دورههایی با تغییرات دما بسیار بالاتر را تجربه میکند. از طرف دیگر، توپ بولینگ دارای دوره گرمایش سریع حدود ده هزار درجه سانتیگراد در ثانیه است. با جرم بیشتری که دارد، سرعت توپ بولینگ میتواند قبل از برخورد با هوای بسیار متراکمتر نزدیک به زمین، به شدت افزایش یابد. این امر موجب افزایش مقاومت هوا و تغییر سریع دما میشود. بهاینترتیب، اگر توپ بولینگ از فضا به زمین بیفتد، ممکن است واقعا آب شود. حیف که سوسک، توپ بولینگ نیست!
































نظرات کاربران